Micrómetro Cronométrico (método del tránsito)

El Micrómetro Cronométrico es el más ampliamente difundido y usado entre los aficionados a la Astronomía y se basa en la rotación aparente de la esfera celeste. Consiste esencialmente en un transportador de plástico que, rectificado, permanece fijo en el portaocular; en su interior gira libremente un pequeño tubo, al que se le ha soldado un disco de acrílico transparente del mismo diámetro que el transportador, y en el que se ha trazado una línea radial (a modo de dial) para la lectura de ángulos, y fijo a este ultimo disco está ubicado el ocular reticulado.

El primer paso en este trabajo, muy importante por cierto, consiste en la ubicación de los puntos cardinales dentro del campo del ocular reticulado, que deben conocerse con la mayor exactitud posible:

• Moviendo el tubo del telescopio hacia el Norte ( geográfico ), veremos por el ocular que la imagen se desplaza hacia el Sur y entra en el campo el Norte.
• Moviendo el tubo del telescopio hacia el Oeste ( geográfico ), veremos por el ocular que la imagen se desplaza hacia el Este y entra en el campo el Oeste; también, al detener la relojería del telescopio (el motor del eje polar), veremos que la imagen se mueve hacia el Oeste.

Es recomendable tener un sistema de relojería electrónica precisa en RA para controlar a intervalos de 30 minutos la ubicación de estos puntos cardinales dentro del campo del ocular, debido a que difícilmente el instrumental esté correctamente "puesto en estación", es decir, que la montura previamente nivelada posea su eje horario exactamente paralelo al eje de rotación de la Tierra. Para determinar la dirección E-W ( oeste en inglés se dice West ) deslizamos la imagen de la estrella sobre el hilo E-W desde un borde del ocular al otro ( relojería apagada ), corrigiendo simultáneamente la posición de dicho hilo ( respecto de la dirección de desplazamiento de la estrella ) rotando el ocular, previendo que dicho astro pase por el centro del ocular; luego, el Norte está a 90° de la dirección hallada ( obviamente del lado del ocular donde se determinó, en la primera aproximación, que quedaba el Norte ). Como muy difícilmente el Norte coincide con el dial en el ángulo 0° del transportador, al ángulo del transportador que indique el sentido Norte lo llamaremos X0 ( y éste ángulo X0 será entonces el origen de los PA de nuestras observaciones).

Desde ya, se recomienda realizar más de 3 mediciones del PA y AS y luego promediarlas, para reducir los errores personales cometidos en las mismas. En este método juegan un papel fundamental la experiencia del observador, su buen estado fisiológico y una noche sin turbulencias ni movimientos en el telescopio.

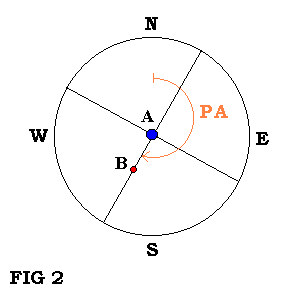
El PA se mide centrando a la componente primaria en el retículo, rotando al disco de acrílico ( que hace rotar al ocular ) hasta que ambas componentes queden ocultadas simultáneamente detrás de un mismo hilo del ocular, obteniendo un nuevo ángulo ( indicado en el transportador por el dial del acrílico ) que llamaremos X1. Luego, el ángulo PA es el desplazamiento ( X0 – X1 ), rotación que sufrió el acrílico:

PA = ABS ( X0 – X1 )      ( ecuación 1 )

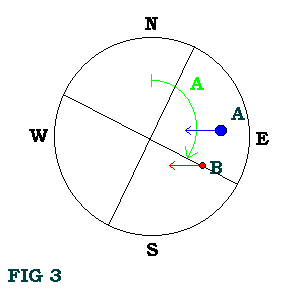
Para obtener la AS, debemos cronometrar el tiempo (t) en segundos que invierten ambas componentes en cruzar, con la relojería momentáneamente detenida, un mismo hilo del retículo ( ver Fig. 3 y Fig. 4 ).

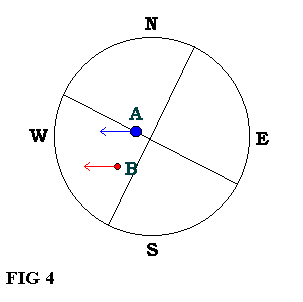
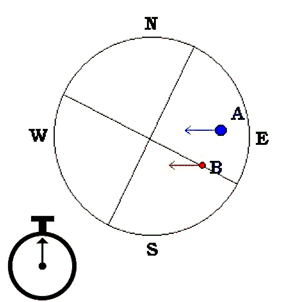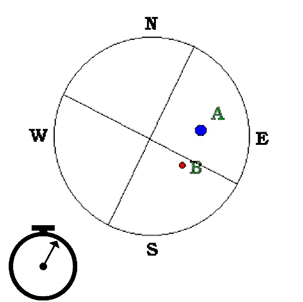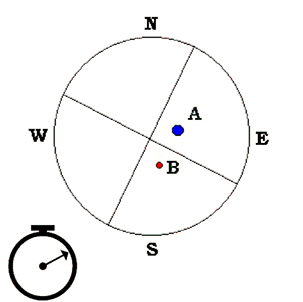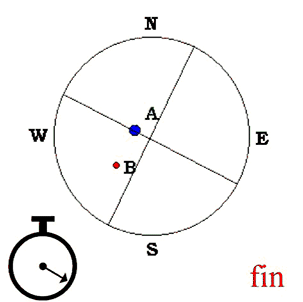
Si el PA=90° ó PA=270° entonces coinciden (se superponen) la dirección del movimiento aparente de los dos astros, lo que implica que la AS la podamos obtener mediante la sencilla fórmula de Movimiento Uniforme del Cielo:

AS = w * t * cos ( Dec )      ( ecuación 2 )

donde w es la velocidad angular aparente de la bóveda celeste, aproximadamente 15.04 "/seg., (t) es el tiempo que las dos componentes necesitan para cruzar el hilo del retículo, y Dec es la declinación del sistema para el equinoccio del instante de observación; mediante el cos (Dec) establecemos la longitud del arco que separa a las estrellas, conocido el ángulo (w)*(t).

Pero como es improbable que suceda lo dicho hasta ahora, debemos rotar mediante el acrílico al hilo en un ángulo arbitrario que llamaremos A ( ver Fig. 3 ), con el objeto de que las estrellas tarden el mayor tiempo t posible en cruzarlo y, por ende, disminuyan los errores:

Tabla 1:

• Si el PA pertenece al 1° ó 3° cuadrante, A debe ser mayor que 90°.
• Si el PA pertenece al 2° ó 4° cuadrante, A debe ser menor que 90°.

donde el ángulo A se mide igual que el PA ( desde el Norte y hacia el Este ). La AS la obtenemos a partir de una de las siguientes ecuaciones, deducidas simplemente a través del teorema del seno y de las cuales, en todos lo libros, usualmente se da la última de ellas :

Tabla 2:

• Si el PA pertenece al 1° cuadrante:
  
  AS = w * t * cos ( Dec ) * ( -cos (A) / sin ( A – PA ) )      ( ecuación 3 )
• Si el PA pertenece al 2° cuadrante:
  
  AS = w * t * cos ( Dec ) * (cos (A) / sin ( PA – A ) )      ( ecuación 4 )
• Si el PA pertenece al 3° cuadrante:
  
  AS = w * t * cos ( Dec ) * ( -cos (A) / sin ( PA – A ) )      ( ecuación 5 )
• Si el PA pertenece al 4° cuadrante
  
  AS = w * t * cos ( Dec ) * (cos (A) / sin ( A - PA ) )      ( ecuación 6 )

Ejemplo:

El día 16 de Julio de 1991 a las 1.28 hs UT, observamos a la estrella doble Alfa Centauri. Primero ubicamos en forma aproximada los puntos cardinales en el campo del ocular , y posteriormente determinamos la dirección E-W ( en consecuencia el Norte ); obtenemos entonces un ángulo arbitrario X0. Luego de medir 3 ángulos X1 establecemos mediante la ecuación (1) los siguientes PA:

PA1 = 215°30'

PA2 = 215°32'

PA3 = 215°28'

, que en promedio dan un PA=215°30' (215º.5); después procedemos a rotar los hilos del retículo en un ángulo A=100° ( lo recomienda la Tabla 1, según el PA obtenido ), tras lo cual toma los tiempos:

t1 = 13.45 seg.

t2 = 14.14 seg.

t3 = 14.23 seg.

, que en promedio dan un t=13.94 seg. Usando la fórmula (5) ( dado que el PA pertenece al 3° cuadrante ) y considerando que la Dec. vale, aproximadamente, -60°48'31.7" (-60º.8088), se obtiene una AS=19.67".

Pero es digno de considerar una sutil corrección a nuestras mediciones, según recomienda Danjon,A en su libro "Astronomie Générale" ( 1952-1953, Paris, pag. 42 ):

x = [ w * t * cos ( Dec ) ] * PI / 3600 / 180       ( ecuación 7 )

Sec( Dec ) = 1 / cos( Dec )       ( ecuación 8 )

DH = [x * Sec( Dec ) + {x3 * Sec3( Dec ) * ( (sin2( Dec ))/2 –1/3 ) } ]       ( ecuación 9 )

t = [ DH ] * 180 * 3600 / PI / w ( tiempo cronometrado corregido )       ( ecuación 10 )

debido a que, a medida que nos aproximamos a los polos celestes, las estrellas no describen líneas rectas sino curvas y entonces nosotros cronometramos el tiempo (t) que ambas tardan en trazar dicha curva, razón por la cual debemos transformar dicho tiempo (t) a cierto tiempo (t-ideal) (situación en la cual las componentes describirían una línea recta ).

Admitamos también que las mediciones hechas con un Micrómetro Filar o una Cámara CCD son más precisas que aquellas hechas con el Micrómetro Cronométrico o el Micrómetro Angular.