Micrómetro Angular
Este nuevo método de medición de estrellas dobles visuales, una variante del Micrómetro Cronométrico, no se basa en la rotación terrestre, aunque utiliza el mismo equipo que el Micrómetro Cronométrico. Ha sido inventado por Alejandro Eduardo Russo a comienzos del año 1991.
Tanto el PA como la AS se miden utilizando sólo el transportador.
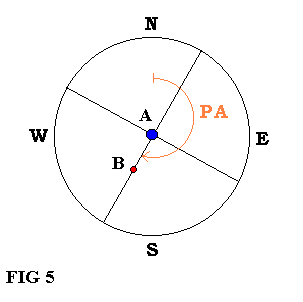
Para encontrar el PA de la estrella binaria, seguimos los mismos procedimientos que con el Micrómetro Cronométrico ( ver Fig. 5 ).
Pero para la AS debemos conocer, con la máxima precisión y exactitud posible, el "Radio del Campo del Telescopio" (R), el cual es igual a la mitad del "Campo Verdadero de Visión" (cvv). Una vez obtenido R, su valor servirá para posteriores trabajos. Este valor de R debe basarse inevitablemente en la rotación aparente del cielo, salvo muy raros casos en los cuales se conoce el "Campo del Ocular" (Co) dado por el fabricante, y el Aumento (M) del telescopio (que recomiendo superior a 200 X ):
cvv = Co / M ( ecuación 11 )
R = Co / ( 2 * M ) ( ecuación 12 )
Pero como el Co usualmente es digno de desconfianzas, o sea no es preciso, debemos poner en práctica la primera opción sugerida: con relojería detenida (el motor del eje polar del telescopio detenido) y utilizando cualquier estrella simple, previendo que pase por el centro del ocular reticulado, cronometramos el tiempo (t), en segundos, que ésta tarda en ir desde el borde Este al Oeste del campo del ocular. Aconsejo realizar esta medición con la máxima seriedad posible, previendo que no haya fuertes vientos que hagan vibrar al tubo del telescopio, que no haya turbulencia atmosférica ( que perjudique la visibilidad nítida del astro ), que el observador se encuentre en óptimo estado ( relajado, cómodo y atento ), y tomar una gran cantidad de cronometrajes del evento ya descripto ( en lo posible más de 30 ) y para disminuir errores elegir una estrella lo más próximo al Ecuador Celeste ).
Si convenimos en que "w" representa la velocidad aparente de la Esfera Celeste, entonces sabemos que w =15.04"/sec aproximadamente. La Dec es la Declinación de la doble para el equinoccio al instante de la medición. Entonces, el "Campo de Visión Verdadera" (cvv) en grados es:
cvv = [ w * t * cos ( Dec ) ] / 3600 ( ecuación 13 )
R = cvv / 2 ( ecuación 14 )
En cambio, los siguientes pasos deben realizarse en cada medición.
Conocido el PA y el cuadrante del sistema deducimos, de acuerdo a la Tabla III, el valor del ángulo P, que es el complemento del primero y sirve para justificar la ecuación del Micrómetro Angular.
Tabla III:
- 1° cuadrante: si PA < 45° -> P = 90° - PA , medición sobre la dirección E-W.
- 1° cuadrante: si PA > 45° -> P = PA , medición sobre la dirección N-S.
- 2° cuadrante: si PA < 135° -> P = 180° - PA , medición sobre la dirección N-S.
- 2° cuadrante: si PA > 135° -> P = PA - 90° , medición sobre la dirección E-W.
- 3° cuadrante: si PA < 225° -> P = 270° - PA , medición sobre la dirección E-W.
- 3° cuadrante: si PA > 225° -> P = PA - 180° , medición sobre la dirección N-S.
- 4° cuadrante: si PA < 315° -> P = 360° - PA , medición sobre la dirección N-S.
- 4° cuadrante: si PA > 315° -> P = PA - 270° , medición sobre la dirección E-W.
El método del Micrómetro Angular consiste en desplazar a la componente A a través del centro del campo del ocular y sobre la dirección E-W ó N-S ( en relación a P y a consideración de la Tabla III ), hasta que la componente B toque el borde del campo del ocular reticulado; una vez hecho esto, usando el transportador medimos el ángulo S, en grados, ángulo formado por las componentes A y B con el centro del retículo tomado como vértice del ángulo ( ver Fig. 6 ).
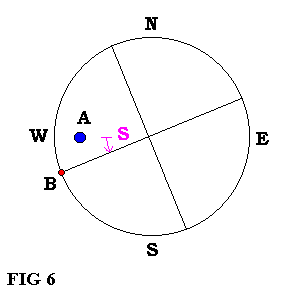
Conocido el valor del ángulo S, usamos la siguiente ecuación para calcular AS:
AS = [ sin (S) * R ] / sin (P) (equación 15)
, donde AS está dada en grados si S está expresada en grados (de hecho, depende de la unidad del R ).
Ejemplo:
El día 3 de Noviembre de 1991 a las 6 hs U.T., observamos a la estrella doble Dun 5. Después de determinar la dirección exacta E-W, determinamos el ángulo X0, el punto Norte en nuestro transportador. Entonces tomamos 3 PA medidos, y, usando la fórmula (1), obtenemos un promedio PA = 191º.0 . Ahora establecemos, usando el PA medido y su cuadrante, el valor de P acorde a la Table III. Esta nos da un ángulo P = 79º.0 (medición en la dirección E-W). Por otro lado, sabemos que R = 00º 04' 44.4" (0º.079), usando las ecuaciones (13) y (14). Por consiguiente, movemos a la componente A en la dirección E-W hasta que la componente B toque el borde el campo del ocular, como se muestra en Fig 6. Medimos el ángulo S = 02º 15' (2º.25), y, usando la fórmula (15), obtenemos nuestra respuesta en grados si R está expresada en grados.
AS = [ sin (2º.250)*(0º.079)] / sin (79º.000)
AS = [ (0.03925982)*(0.079)] / (0.98162719)
AS = 0º.00315968
AS = (0º.00315968)*(3600) = 11".37
AS = 11".37
Ventajas: La principal ventaja reside, esencialmente, en que cada medición es completamente independiente de la Declinación del sistema observado.
Desventajas: si el error en la medición del ángulo PA (leído en el transportador) es grande, en consecuencia el error final de la AS será grande.
Pero a pesar de este inconveniente, el nuevo método dá un respiro a aquellos aficionados que no tienen habilidad, porque en lugar de velocidad en la coordinación vista-cronómetro se requiere, eso sí, una gran destreza en ubicar a la componente B en el borde del campo del ocular reticulado.
Admitamos también que las mediciones hechas con un Micrómetro Filar o una Cámara CCD son más precisas que aquellas hechas con el Micrómetro Cronométrico o el Micrómetro Angular.
