Angular Micrometer

This new method of measuring visual double stars, a variant of the Chronometric Micrometer, is not based on the Earh´s rotation, but uses the same equipment as the Chronometric Micrometer. It was invented by Alejandro Eduardo Russo at the beginning of the year 1991.

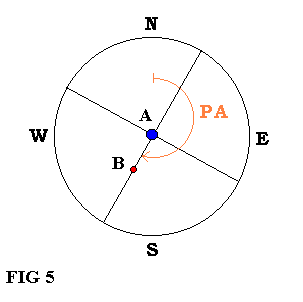
As the PA as the ACE are measured only using the protractor.

To find the PA of the binary star, we follow the same procedure as with the Chronometric Micrometer. (to see Fig. 5).

However, for the AS, we must know with the maximum precision and exactness possible, the "Ratio of the Field of the Telescope" (R), which is equal to half of the "true field of view" (tfv). Once it is obtained, which is done only once, it should be good for all future work. This value must inevitably be based on the apparent rotation of the sky, except in those rare cases where we know the exact "apparent field of view" (afv) of the eyepiece, as given by the manufacturer, and the Magnification (M) of the telescope (recommended at 200x or more).

cvv = Co / M       ( equation 11 )

R = Co / ( 2 * M )       ( equation 12 )

If you suspect that the value given for the apparent field of view of your eyepiece may not be accurate, we must look to the first option: with the telescope´s drive off, select any star and allow it to pass through the center of the reticle eyepiece, noting the time (t) in seconds that the selected star took to travel from the East edge to the West edge of the eyepiece´s field. I recommend doing this measurements for maximum accuracy by taking a large number of measurements of the transit time (t) needed for the selected star to cross the eyepiece´s entire field of view. If possible, 30 or more timings are recommended. To decrease errors, select a star near the celestial equator. Select a night: without strong winds (that make to vibrate to the tube of the telescope), that there are not atmospheric turbulence (damage the clear visibility of the star), and that the observer is relaxed, comfortable and attentive.

If we agree that "w" represents the apparent velocity of the celestial sphere, then we know that w =15.04"/sec approximately. The Dec is the Declination of the double for the equinox at the time of measurement. Therefore, the true field of view (tfv) in degrees is:

cvv = [ w * t * cos ( Dec ) ] / 3600       ( equation 13 )

R = cvv / 2       ( equation 14 )

On the other hand, the following procedures should be followed for each measurement.

Knowing the PA and the quadrant of the pair, we can deduce, looking at Table III, the value of angle P that this is the complement of the PA and it is useful for to justify the equation of the "angular micrometer"

Table III:

• 1st quadrant: if PA < 45° -> P = 90° - PA, measurement in E-Wdirection.
• 1st quadrant: if PA > 45° -> P = PA, measurement in N-S direction.
• 2nd quadrant: if PA < 135° -> P = 180° - PA, measurement in N-S direction.
• 2nd quadrant: if PA > 135° -> P = PA - 90°, measurement in E-W direction.
• 3rd quadrant: if PA < 225° -> P = 270° - PA, measurement in E-W direction.
• 3rd quadrant: if PA > 225° -> P = PA - 180°, measurement in N-S direction.
• 4th quadrant: if PA < 315° -> P = 360° - PA, measurement in N-S direction.
• 4th quadrant: if PA > 315° -> P = PA - 270°, measurement in E-W direction.

The method of using the "Angular Micrometer" consists of moving component A through the center of the field in the E-W or N-S direction (in relation to P and according to Table III), until the component B touches the border of the reticle eyepiece´s field, as is illustrated in fig 6. Using the protractor, we measure angle (S) in degrees. This is the angle formed by the components A and B, with the center of the reticle taken as the vertex of the angle (see fig 6).

Known the value of angle S, we use the following equation to calculate the AS:

AS = [ sin (S) * R ] / sin (P)       (equation 15)

, where AS is given in degrees if R is in degrees (in fact, it depends on the unit of the R).

Example:

On 3 November 1991 at 6:00 UT, we observe the double star Dun 5. After determining the exact E-W direction, we determine the angle X0, the north point on our protractor. We then take three position angle measurements, and, using formula (1), we obtain an average PA = 191º.0 . We now establish, using the PA measurement and its quadrant location, the value of P according to Table III. This gives us the angle P = 79º.0 (measured in the E-W direction). We know that R = 00º 04' 44.4" (0º.079), using equations (13) and (14). Therefore, we move the A component in the E-W direction until the B component touches the border of the eyepiece field of view, as shown in Fig 6. We measure angle S = 02º 15' (2º.25), and, using formula (15), we obtain our answer in degrees if R is in degrees.

AS = [ sin (2º.250)*(0º.079)] / sin (79º.000)

AS = [ (0.03925982)*(0.079)] / (0.98162719)

AS = 0º.00315968

AS = (0º.00315968)*(3600) = 11".37

AS = 11".37

Advantages: The principal advantage resides, essentially, in that each measurement is completely independent of the Declination of the observed system.

Disadvantages: if the error in the measurement of the angle PA (read in the protractor) is big, in consequence the final error of the AS will be big.

But in spite of the inconvenience, the "new" method gives a respiration to some amateurs that not have ability, because instead of speed in the view-chronometer coordination is required, of course, a great dexterity in locating the component B in the border of the eyepiece field of view.

Admittedly, we must realize that measurements made with a filar micrometer and the CCD are generally more accurate than those made with the chronometric micrometer (transit method) or the angular micrometer.